Программы на С++ с использованием технологии OpenMP
Умножение матриц
Ниже приведена тестовая программа умножения матриц. В этой программе есть функция обычного умножения и функция с использованием технологии OpenMP.
#include <iostream>
#include <omp.h>
#include <time.h>
#include <math.h>
using namespace std;
//Функция параллельного умножения матриц с использованием технологии OpenMP
void umn_matr_parallel(float**A,float**B,float**C , int N)
{
#pragma omp parallel for shared(A, B, C)
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
C[i][j] = 0.0;
for(int k=0; k<N; k++) C[i][j]+=A[i][k]*B[k][j];
}
}
}
//Функция стандартного умножения матриц
void umn_matr(float**A,float**B, float**C , int N)
{
//#pragma omp parallel for shared(A, B, C) private (i,j,k)
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
C[i][j] = 0.0;
for(int k=0; k<N; k++) C[i][j]+=A[i][k]*B[k][j];
}
}
}
int main()
{
int i, j, k, N;
cin>>N;
cout<<"В системе "<<omp_get_num_procs()<<" процессора"<<endl;
float**a, **b, **c;
a=new float*[N];
for(i=0;i<N;i++)
a[i]=new float[N];
b=new float*[N];
for(i=0;i<N;i++)
b[i]=new float [N];
c=new float*[N];
for(i=0;i<N;i++)
c[i]=new float[N];
float t1, t2, tn, tk;
// инициализация матриц
for ( i=0; i<N; i++)
for ( j=0; j<N; j++)
a[i][j]=b[i][j]=sin(i)*cos(j);
cout<<"СТАРТ!!!\n";
tn=omp_get_wtime();
umn_matr(a,b,c,N);
tk=omp_get_wtime();
cout<<"Время последовательного счёта="<<tk-tn<<endl;
t1=omp_get_wtime();
umn_matr_parallel(a,b,c,N);
t2=omp_get_wtime();
cout<<"Время параллельного счёта="<<t2-t1<<endl;
}
Тестирование программы проходило на ПК с материнской платой MSI H67MA-E45, процессор Intel Core I5 (3.3 Ггц), ОЗУ 4 Гб, ОС Xubuntu 11.10 c pae ядром, компилятор g++ 4.6.
Результаты тестирования представлены в таблице 1 и на рис. 1.
Ниже приведена тестовая программа умножения матриц. В этой программе есть функция обычного умножения и функция с использованием технологии OpenMP.
#include <iostream>
#include <omp.h>
#include <time.h>
#include <math.h>
using namespace std;
//Функция параллельного умножения матриц с использованием технологии OpenMP
void umn_matr_parallel(float**A,float**B,float**C , int N)
{
#pragma omp parallel for shared(A, B, C)
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
C[i][j] = 0.0;
for(int k=0; k<N; k++) C[i][j]+=A[i][k]*B[k][j];
}
}
}
//Функция стандартного умножения матриц
void umn_matr(float**A,float**B, float**C , int N)
{
//#pragma omp parallel for shared(A, B, C) private (i,j,k)
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
C[i][j] = 0.0;
for(int k=0; k<N; k++) C[i][j]+=A[i][k]*B[k][j];
}
}
}
int main()
{
int i, j, k, N;
cin>>N;
cout<<"В системе "<<omp_get_num_procs()<<" процессора"<<endl;
float**a, **b, **c;
a=new float*[N];
for(i=0;i<N;i++)
a[i]=new float[N];
b=new float*[N];
for(i=0;i<N;i++)
b[i]=new float [N];
c=new float*[N];
for(i=0;i<N;i++)
c[i]=new float[N];
float t1, t2, tn, tk;
// инициализация матриц
for ( i=0; i<N; i++)
for ( j=0; j<N; j++)
a[i][j]=b[i][j]=sin(i)*cos(j);
cout<<"СТАРТ!!!\n";
tn=omp_get_wtime();
umn_matr(a,b,c,N);
tk=omp_get_wtime();
cout<<"Время последовательного счёта="<<tk-tn<<endl;
t1=omp_get_wtime();
umn_matr_parallel(a,b,c,N);
t2=omp_get_wtime();
cout<<"Время параллельного счёта="<<t2-t1<<endl;
}
Тестирование программы проходило на ПК с материнской платой MSI H67MA-E45, процессор Intel Core I5 (3.3 Ггц), ОЗУ 4 Гб, ОС Xubuntu 11.10 c pae ядром, компилятор g++ 4.6.
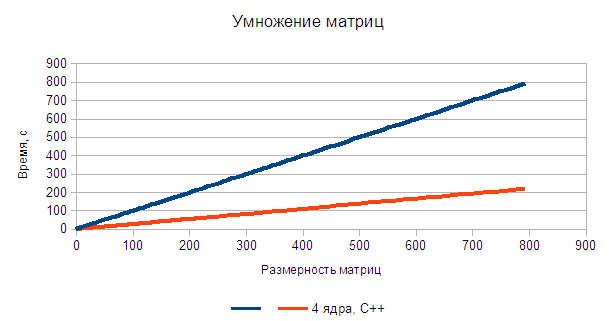
Результаты тестирования представлены в таблице 1 и на рис. 1.
Таблица 1.
| Время, с | Размерность матрицы | 200 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 |
| 1 ядро, С++ | 0.034 | 0.55 | 10.38 | 36.24 | 88.49 | 179.28 | 321.63 | 514.68 | 792.13 | |
| 4 ядра, С++ | 0.006 | 0.14 | 2.62 | 9.43 | 23.11 | 49.19 | 87.75 | 143.31 | 218.86 |

Рисунок 1
Решение СЛАУ методом простой итерации
Ниже приведена тестовая программа решения СЛАУ, система уравнений формировалась, удовлетворяющая условию сходимости, с диагональным преобладанием. В этой программе есть функции обычного и параллельного (с использованием технологии OpenMP) решения СЛАУ методом простой итерации.
#include <iostream>
#include <math.h>
#include <omp.h>
using namespace std;
float form_jacobi(float **alf,float *x, float *x1, float *bet, int n)
{
int i,j;
float s,max;
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x1[i]=s;
}
return max;
}
float form_jacobi_parallel(float **alf,float *x, float *x1, float *bet, int n)
{
int i,j;
float s,max;
#pragma omp parallel for shared(alf, bet, x,x1) private (i,j,s)
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x1[i]=s;
}
return max;
}
//Функция, реализующая распараллеленный метод простой итерации (точность //вычислений eps)
int jacobi_parallel(float **a, float *b, float *x, int n, float eps)
{
float **f, *h, **alf, *bet, *x1, *xx, s, s1, max; int i,j,k,kvo;
float t1, t2;
cout<<"\n Распараллеленный метод Якоби"<<endl;
f=new float *[n];
for(i=0;i<n;i++)
f[i]=new float[n];
h=new float [n];
alf=new float *[n];
for(i=0;i<n;i++)
alf[i]=new float[n];
bet=new float [n];
x1=new float [n];
xx=new float [n];
cout<<"\n СТАРТ"<<endl;
//cout<<"\n Вектор h"<<endl;
#pragma omp parallel for private (i,j)
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
if (i==j) alf[i][j]=0; else alf[i][j]=-a[i][j]/a[i][i];
bet[i]=b[i]/a[i][i];
}
for(i=0;i<n;i++)
x1[i]=bet[i];
kvo=0;max=5*eps;
cout<<"\n Старт итерационного процесса"<<endl;
t1=omp_get_wtime();
while(max>eps)
{
for(i=0;i<n;i++)
x[i]=x1[i];
max=form_jacobi_parallel(alf, x, x1,bet, n);
kvo++;
}
t2=omp_get_wtime();
cout<<"Время итерационного процесса"<<t2-t1<<endl;
cout<<"\nmax="<<max<<"\tkvo="<<kvo<<"\teps="<<eps<<endl;
return kvo;
}
//Функция, реализуящая обычный метод простой итерации (точность вычислений eps)
int jacobi(float **a, float *b, float *x, int n, float eps)
{
float **f, *h, **alf, *bet, *x1, *xx, s, s1, max; int i,j,k,kvo;
float t1,t2;
cout<<"\n Метод Якоби"<<endl;
f=new float *[n];
for(i=0;i<n;i++)
f[i]=new float[n];
h=new float [n];
alf=new float *[n];
for(i=0;i<n;i++)
alf[i]=new float[n];
bet=new float [n];
x1=new float [n];
xx=new float [n];
cout<<"\n СТАРТ"<<endl;
for(i=0;i<n;bet[i]=b[i]/a[i][i],i++)
for(j=0;j<n;j++)
if (i==j) alf[i][j]=0; else alf[i][j]=-a[i][j]/a[i][i];
for(i=0;i<n;i++)
x1[i]=bet[i];
kvo=0;max=5*eps;
cout<<"\n Старт итерационного процесса"<<endl;
t1=omp_get_wtime();
while(max>eps)
{
for(i=0;i<n;i++)
x[i]=x1[i];
max=form_jacobi(alf,x,x1,bet,n);
kvo++;
}
t2=omp_get_wtime();
cout<<"Время итерационного процесса"<<t2-t1<<endl;
cout<<"\nmax="<<max<<"\tkvo="<<kvo<<"\teps="<<eps<<endl;
return kvo;
}
float form(float **alf,float *x, float *bet, int n)
{
int i,j;
float s,max;
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x[i]=s;
}
return max;
}
float form_parallel(float **alf,float *x, float *bet, int n)
{
int i,j;
float s,max;
#pragma omp parallel for shared(alf, bet, x) private (i,j,s)
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x[i]=s;
}
return max;
}
int main(int argc, char **argv)
{
int result,i,j,N;
float **a, *b, *x,s, t1parl,t2parl,t1posl,t2posl, ep;
clock_t t1,t2;
cout<<"N=";
cin>>N;
ep=1e-6;
a=new float *[N];
for(i=0;i<N;i++)
a[i]=new float[N];
b=new float [N];
x=new float [N];
cout<<"Input Matrix A"<<endl;
for(i=0;i<N;a[i][i]=1,i++)
for(j=0;j<N;j++)
if (i!=j) a[i][j]=0.1/(i+j);
for(i=0;i<N;i++) b[i]=sin(i);
cout<<"Матрица A занимает"<<N*N*sizeof(float)<<"байт"<<endl;
cout<<"Матрица A занимает"<<N*N*sizeof(float)/1024/1024<<"Мбайт"<<endl;
cout<<"Массив B занимает"<<N*sizeof(float)<<"байт"<<endl;
cout<<"Массив В занимает"<<N*sizeof(float)/1024/1024<<"Мбайт"<<endl;
cout<<"МЕТОД ЯКОБИ, СТАРТ!!!\n";
t1posl=omp_get_wtime();
cout<<jacobi(a,b,x,N,ep);
t2posl=omp_get_wtime();
cout<<"\nВремя последовательного счёта методом Якоби="<<t2posl-t1posl<<endl;
cout<<"\n Вектор X"<<endl;
cout<<x[0]<<"\t"<<x[N/2]<<"\t"<<x[N-1];
cout<<endl;
cout<<"ПАРАЛЛЕЛЬНЫЙ МЕТОД ЯКОБИ, СТАРТ!!!\n";
t1parl=omp_get_wtime();
cout<<jacobi_parallel(a,b,x,N,ep);
t2parl=omp_get_wtime();
cout<<"\n Вектор X"<<endl;
cout<<x[0]<<"\t"<<x[N/2]<<"\t"<<x[N-1];
cout<<endl;
cout<<"\nВремя параллельного счёта методом Якоби="<<t2parl-t1parl<<endl;
return 0;
}
Тестирование программы проходило на ПК с материнской платой MSI H67MA-E45, процессор Intel Core I5 (3.3 Ггц), ОЗУ 4 Гб, ОС Xubuntu 11.10 c pae ядром, компилятор g++ 4.6.
Результаты тестирования представлены в таблице 2 и на рис. 2.
Таблица 2.
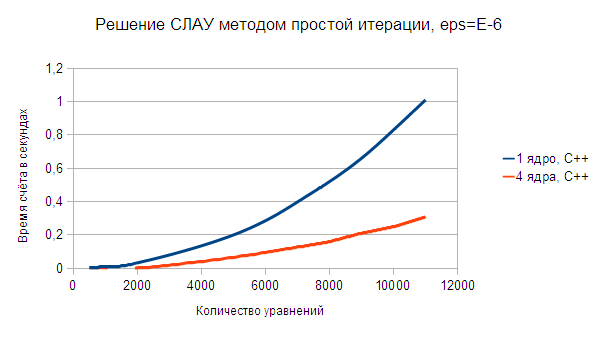
Рисунок 2
Ниже приведена тестовая программа решения СЛАУ, система уравнений формировалась, удовлетворяющая условию сходимости, с диагональным преобладанием. В этой программе есть функции обычного и параллельного (с использованием технологии OpenMP) решения СЛАУ методом простой итерации.
#include <iostream>
#include <math.h>
#include <omp.h>
using namespace std;
float form_jacobi(float **alf,float *x, float *x1, float *bet, int n)
{
int i,j;
float s,max;
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x1[i]=s;
}
return max;
}
float form_jacobi_parallel(float **alf,float *x, float *x1, float *bet, int n)
{
int i,j;
float s,max;
#pragma omp parallel for shared(alf, bet, x,x1) private (i,j,s)
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x1[i]=s;
}
return max;
}
//Функция, реализующая распараллеленный метод простой итерации (точность //вычислений eps)
int jacobi_parallel(float **a, float *b, float *x, int n, float eps)
{
float **f, *h, **alf, *bet, *x1, *xx, s, s1, max; int i,j,k,kvo;
float t1, t2;
cout<<"\n Распараллеленный метод Якоби"<<endl;
f=new float *[n];
for(i=0;i<n;i++)
f[i]=new float[n];
h=new float [n];
alf=new float *[n];
for(i=0;i<n;i++)
alf[i]=new float[n];
bet=new float [n];
x1=new float [n];
xx=new float [n];
cout<<"\n СТАРТ"<<endl;
//cout<<"\n Вектор h"<<endl;
#pragma omp parallel for private (i,j)
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
if (i==j) alf[i][j]=0; else alf[i][j]=-a[i][j]/a[i][i];
bet[i]=b[i]/a[i][i];
}
for(i=0;i<n;i++)
x1[i]=bet[i];
kvo=0;max=5*eps;
cout<<"\n Старт итерационного процесса"<<endl;
t1=omp_get_wtime();
while(max>eps)
{
for(i=0;i<n;i++)
x[i]=x1[i];
max=form_jacobi_parallel(alf, x, x1,bet, n);
kvo++;
}
t2=omp_get_wtime();
cout<<"Время итерационного процесса"<<t2-t1<<endl;
cout<<"\nmax="<<max<<"\tkvo="<<kvo<<"\teps="<<eps<<endl;
return kvo;
}
//Функция, реализуящая обычный метод простой итерации (точность вычислений eps)
int jacobi(float **a, float *b, float *x, int n, float eps)
{
float **f, *h, **alf, *bet, *x1, *xx, s, s1, max; int i,j,k,kvo;
float t1,t2;
cout<<"\n Метод Якоби"<<endl;
f=new float *[n];
for(i=0;i<n;i++)
f[i]=new float[n];
h=new float [n];
alf=new float *[n];
for(i=0;i<n;i++)
alf[i]=new float[n];
bet=new float [n];
x1=new float [n];
xx=new float [n];
cout<<"\n СТАРТ"<<endl;
for(i=0;i<n;bet[i]=b[i]/a[i][i],i++)
for(j=0;j<n;j++)
if (i==j) alf[i][j]=0; else alf[i][j]=-a[i][j]/a[i][i];
for(i=0;i<n;i++)
x1[i]=bet[i];
kvo=0;max=5*eps;
cout<<"\n Старт итерационного процесса"<<endl;
t1=omp_get_wtime();
while(max>eps)
{
for(i=0;i<n;i++)
x[i]=x1[i];
max=form_jacobi(alf,x,x1,bet,n);
kvo++;
}
t2=omp_get_wtime();
cout<<"Время итерационного процесса"<<t2-t1<<endl;
cout<<"\nmax="<<max<<"\tkvo="<<kvo<<"\teps="<<eps<<endl;
return kvo;
}
float form(float **alf,float *x, float *bet, int n)
{
int i,j;
float s,max;
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x[i]=s;
}
return max;
}
float form_parallel(float **alf,float *x, float *bet, int n)
{
int i,j;
float s,max;
#pragma omp parallel for shared(alf, bet, x) private (i,j,s)
for(i=0;i<n;i++)
{
s=0;
for(j=0;j<n;j++)
s+=alf[i][j]*x[j];
s+=bet[i];
if (i==0) max=fabs(x[i]-s); else if (fabs(x[i]-s)>max) max=fabs(x[i]-s);
x[i]=s;
}
return max;
}
int main(int argc, char **argv)
{
int result,i,j,N;
float **a, *b, *x,s, t1parl,t2parl,t1posl,t2posl, ep;
clock_t t1,t2;
cout<<"N=";
cin>>N;
ep=1e-6;
a=new float *[N];
for(i=0;i<N;i++)
a[i]=new float[N];
b=new float [N];
x=new float [N];
cout<<"Input Matrix A"<<endl;
for(i=0;i<N;a[i][i]=1,i++)
for(j=0;j<N;j++)
if (i!=j) a[i][j]=0.1/(i+j);
for(i=0;i<N;i++) b[i]=sin(i);
cout<<"Матрица A занимает"<<N*N*sizeof(float)<<"байт"<<endl;
cout<<"Матрица A занимает"<<N*N*sizeof(float)/1024/1024<<"Мбайт"<<endl;
cout<<"Массив B занимает"<<N*sizeof(float)<<"байт"<<endl;
cout<<"Массив В занимает"<<N*sizeof(float)/1024/1024<<"Мбайт"<<endl;
cout<<"МЕТОД ЯКОБИ, СТАРТ!!!\n";
t1posl=omp_get_wtime();
cout<<jacobi(a,b,x,N,ep);
t2posl=omp_get_wtime();
cout<<"\nВремя последовательного счёта методом Якоби="<<t2posl-t1posl<<endl;
cout<<"\n Вектор X"<<endl;
cout<<x[0]<<"\t"<<x[N/2]<<"\t"<<x[N-1];
cout<<endl;
cout<<"ПАРАЛЛЕЛЬНЫЙ МЕТОД ЯКОБИ, СТАРТ!!!\n";
t1parl=omp_get_wtime();
cout<<jacobi_parallel(a,b,x,N,ep);
t2parl=omp_get_wtime();
cout<<"\n Вектор X"<<endl;
cout<<x[0]<<"\t"<<x[N/2]<<"\t"<<x[N-1];
cout<<endl;
cout<<"\nВремя параллельного счёта методом Якоби="<<t2parl-t1parl<<endl;
return 0;
}
Тестирование программы проходило на ПК с материнской платой MSI H67MA-E45, процессор Intel Core I5 (3.3 Ггц), ОЗУ 4 Гб, ОС Xubuntu 11.10 c pae ядром, компилятор g++ 4.6.
Результаты тестирования представлены в таблице 2 и на рис. 2.
Таблица 2.
| Время, с | Размерность матрицы | 500 | 1000 | 2000 | 5000 | 7000 | 8000 | 9000 | 10000 | 11000 |
| 1 ядро, С++ | 0.006 | 0.013 | 0.05 | 0.31 | 0.6 | 0.78 | 0.98 | 1.21 | 1.47 | |
| 4 ядра, С++ | 0.004 | 0.006 | 0.018 | 0.11 | 0.19 | 0.25 | 0.33 | 0.38 | 0.44 |

Рисунок 2